Главная » Производная, исследование функций » Нахождение производной
Нахождение производной, Наибольшее и наименьшее значение ф-ции на отрезке, Построение графика функции, Вычисление производной функции в точке, Решение дифференциальных уравнений

Нахождение производной онлайн

Онлайн нахождение производной

Введите функцию f(x) = Найти производную

Установить такой виджет себе на сайт © MathOnline.um-razum.ru


Установить себе на сайт виджет "Нахождение производной"

Нахождение производной

Если вас интересуют общие вопросы и само понятие производной, вы можете посмотреть цикл демонстрационных видеороликов от автора данного сайта Максима Семенихина на тему «Понятие производной».

1. Понятие о скорости возрастания и убывания функции (6:01)
2. Вычисление скорости возрастающей функции (2:05)
3. Вычисление скорости убывающей функции (2:18)
4. На разных промежутках – разная скорость (4:15)
5. Средняя и мгновенная скорости (3:38)
6. Средняя скорость возрастания функции (1:59)
7. Определение производной как скорости (2:50)
8. Пример вычисления производной по определению (3:46)
9. Обозначение производной (1:41)

а также видеоурок

Вычисление производных сложных функций (14:51)

Для нахождения производной функции в общем случае необходимо знать следующее:

1. Таблицу производных элементарных функций.
2. Правила дифференцирования.
3. Как находить производную сложной функции.

Таблица производных элементарных функций представлена ниже:

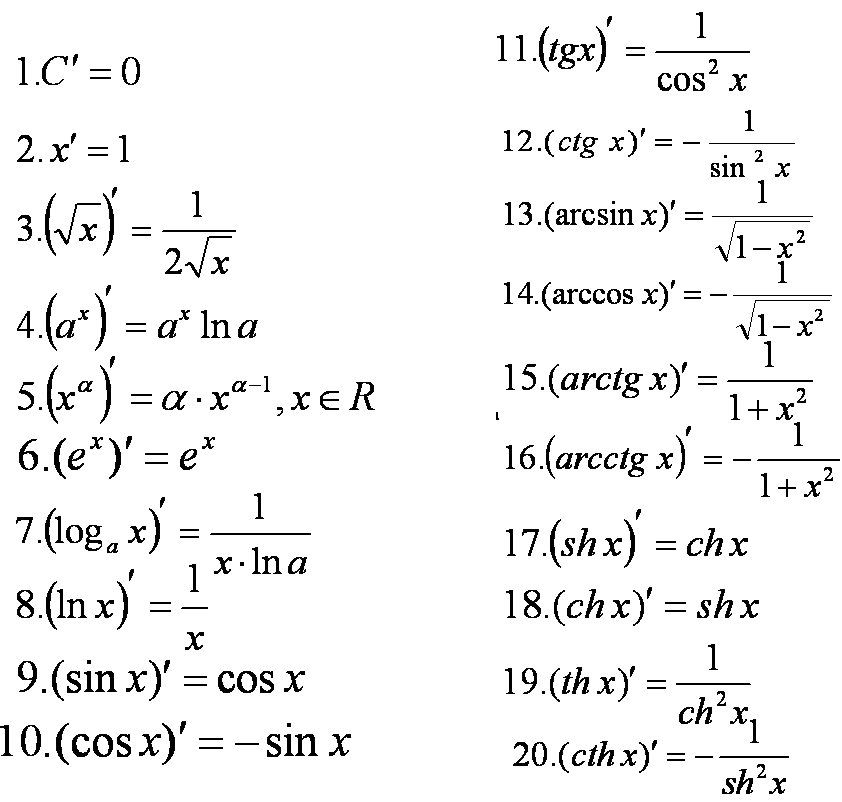
Для нахождения производной суммы, произведения и частного функций используются три правила дифференцирования:

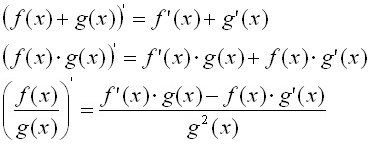
Для нахождения производной сложной функции используется формула

f(g(x))' = f '(g(x)) · g'(x)

Нахождение производной сложной функции – вопрос, заслуживающий отдельного рассмотрения. Вы можете просмотреть видеоурок «Вычисление производных сложных функций».

Онлайн калькулятор
для нахождения производной
любой функции

Для нахождения производной любой функции вы можете воспользоваться калькулятором (виджетом WolframAlpha) вверху страницы. Просто введите функцию в текстовое поле, нажмите кнопку «=» и получите результат.
Для того, чтобы получить пошаговое объяснение нахождению производной, нажмите ссылку «Step-by-step Solution», которая появится после нажатия кнопки «=».